Blog
Introduction to basic techniques for AI (artificial intelligence)

This article gives a quick overview of the techniques behind artificial intelligence applied to abstract strategy games. It also discusses higher-order modules and why they’re interesting for modular composability.
I. Introduction
For some of you, the idea of someday programming an AI for board games / turn-based strategy games isn’t completely foreign — maybe it even came up while you were learning a programming language. But other priorities took over, so you put those projects off. That doesn’t mean you lost interest forever.
There are several reasons your enthusiasm may still be alive:
Programming an AI is fun, honorable, demanding and motivating.
No game-creation software ships with a ready-to-use AI.
Even if a creation tool did include an AI, you rightly feel it wouldn’t be adaptable to the exact game mechanics you want.
Massive gains in computing power have mostly benefited graphics, not AI — and you have the reasonable sense that there’s still a huge margin for improvement toward smarter behavior.
This article builds on your algorithm background to introduce some elementary AI techniques. I’ve deliberately kept the algorithmic level to the bare minimum — partly so it stays readable for everyone, and partly to better introduce higher-order modules, a very promising modeling technique for AI. In many ways, treating modules generically seems as natural to me as treating types generically. I hope the example developed here will be convincing enough to excuse this eccentricity.
II. Where to find AI documentation?
The real question is: “What documentation can I find that will actually be useful to me?”
“Artificial Intelligence” is a broad term covering:
A range of solutions for classic games/problems whose representativeness has driven research that’s mature enough for your game/application to benefit. With some customization (always somewhat artisanal), you should be able to build a convincing AI that presents a real challenge to a human player.
A set of research directions for games/problems that are still actively being studied. Each direction alone is an advance, but some approaches are mutually exclusive by design choices, making it impossible to assemble a fully optimized solution for the problem at hand. In those cases, even the best technical compromise may not hold up versus a highly experienced human player.
The safest route to success is to link your game/problem to a well-known, well-studied classic — for example a pawn game (checkers is the archetype) or a positional game (chess is the archetype). In any case, until you master all the stakes, it’s better to keep researching rather than rush into implementation with little chance of success. As in many moderately complex projects, the ideal situation is when you only have to assemble independent, already well-tested components.
AI documentation can be hard to approach because it’s often not specific enough for your application. That generality has benefits though: it helps you isolate the main components of your AI engine.
Most documentation is in English and splits into two categories:
Beginner tutorials: their main purpose is to clear the ground and ease your progress into the intimidating domain of AI.
Research papers: often hard to read and not necessarily useful for your app. Even when a paper seems close to your concerns, there’s usually a restriction or a design choice that makes it unusable for your project. Read them to harvest concepts and ideas.
In the end, you design the system — nobody hands you a finished solution. Building good AI often requires algorithmic innovation. There’s no universal AI solution — if there were, it would already be bundled in a game-creation package and you wouldn’t need to develop anything. Typically you’ll review a wide panel of technical solutions and mix the cocktail that best fits your application. You’ll also need to identify the “weak link” — the bad component or poor design that drags down performance and quality — and, after finding it, diagnose how to fix it with a more inspired solution.
A must-read beginner tutorial (I know of no better): Chess Programming
An example of a research paper (interesting, but advanced): Solving large combinatorial search spaces
III. Where to start?
Start by reading the Chess Programming tutorial (begin with the “Basics”).
The techniques there are presented for chess, but they’re exactly the same techniques you should apply to any board/strategy game. Read the tutorial — but don’t start by programming a chess game; that’s too hard and introduces too many new concepts at once. In my opinion you shouldn’t even start with a two-player game. To get familiar with the basic techniques, it’s better to start with a solitaire puzzle: an AI that searches for a solution to a puzzle.
IV. Core issues
AI has two enemies:
the breadth (width) of the game;
the depth of the game.
All AI techniques fight these two enemies: they try to curb the inflation of the search space by artificially reducing either its width or its depth. The search space is the set of game positions reachable from a given position. AI performance (whether quality is high or low) will depend primarily on your ability to limit the naturally expansive search space. Whatever the processing power, it can’t handle a combinatorial explosion. So you must ensure that the set of positions actually analyzed by the program is always much smaller than the full search space. In most cases, exhaustive analysis is either unimaginable or impractical for interactive use. AI skill is essentially knowing how to limit the search extent without (too much) compromising the quality of the result.
Roughly, games can be categorized into three types of search spaces:
- Mostly deep games: like Checkers or Chess — only a few possible moves per turn (say at most a couple dozen), but the game can last many dozens of moves.
- Mostly wide games: like pentomino puzzles — the game is short (only a few moves) but each move has dozens or hundreds of possibilities.
- Hard games: like Go — these games are nasty because they’re both wide and deep at the same time.
Basic practices
The most elementary AI skills are:
knowing how to generate possible moves from a game position;
knowing how to fight false width, i.e. redundant branching.
There are two very common causes of redundant width in solitaire games:
1. You do move A then move B, or move B then move A; if both sequences lead to the same game position, you’ve needlessly duplicated work. For example, on a Rubik’s Cube, doing a quarter turn on the front face then a quarter turn on the back face is the same as doing the quarter turn on the back face then the quarter on the front face. You must remove such symmetry or the search space will grow unnecessarily.
2. You do move A then move B, but move B cancels move A and you end up back where you started. Again on a Rubik’s Cube, doing a quarter turn front then a 3/4 turn front results in a full turn and you’re back to the initial position. You must remove such repetitions too.
The most effective way to fight false width is the transposition table technique. A transposition table is the set of game positions already reached by the search. Since it’s a set, it can’t contain duplicates — and that’s what prevents false widening of the search space.
I’ll come back to the transposition table later. For now let’s talk about the board model to make the idea of the search space more concrete.
V. Move generation
Let’s try to model a game board.
A given type of board yields a certain type of moves. In a module language (here Objective Caml), we might express it like this:
*ocaml
module type Board =
sig
type board
type moves
end
*
This reads: there exists a module type named `Board` that contains a `board` type and a `moves` type.
That doesn’t do much yet. It starts to mean something if we add that a game position (`game`) is a record containing:
a `board` field for the board;
a `played` field for the moves played since the initial position.
So we update our module type:
*ocaml
module type Board =
sig
type board
type moves
type game = {board: board; played: moves}
end
*
But it’s not finished. What we want next is to build the search space. For that we need a game strategy:
A game strategy is a function that performs an action on a game — an action is typed `unit`, a game is `game`, so performing an action on a game is `game -> unit`.
This action is not arbitrary: it consists of adding to the transposition table the new positions generated by applying an additional move.
Adding a position is also an action `game -> unit`.
So the complete strategy type is `(game -> unit) -> (game -> unit)`: given the ability to add a game, it returns the ability to add all positions reachable in one move.
That gives us this module type:
*ocaml
module type Board =
sig
type board
type moves
type game = {board: board; played: moves}
type strategy = (game -> unit) -> (game -> unit)
end
*
A module type is like a class type: it’s an interface an implementation module must conform to in order to be recognized as that module type. Conformance is structural: the implementation doesn’t explicitly declare it implements the module type, it just exports an interface that’s structurally a subtype of the desired module type. You can’t use a module type directly — you must implement it first.
With this module type we’re done with boards. Next: the transposition table.

Easy AI Course PocketCube 3D demonstrator
VI. The transposition table
We want a data structure (type `t`) that implements set-like operations over elements (type `item`), specifically:
`empty`: create an empty set;
`singleton`: create a single-element set;
`add`: add a new element (does nothing if the element is already present);
`zip_intersect`: compute the intersection between two transposition tables — the “zip” name comes from using a zipper function ;
`iter`: traverse the whole set and apply the same function to each element.
That’s expressed like this:
*ocaml
module Mutable = struct
module type Set =
sig
type t
type item
val empty: unit -> t
val singleton: item -> t
val add: item -> t -> unit
val zip_intersect: (item -> item -> ‘a) -> t -> t -> ‘a list
val iter: (item -> unit) -> t -> unit
end
end
*
So there’s a module type `Set` with a type `t` of items `item` and operations `empty`, `singleton`, `add`, `zip_intersect`, `iter`.
It’s good to have declared this `Set` module type. Even better if we have a concrete module implementing it. Lucky you — there’s one ready: `MakeSet`.
A few side remarks:
`add` has type `item -> t -> unit`, which suggests it works well as the implementation of a strategy when `item = game`.
`MakeSet` is a parameterized module (a function from a module to a module). Modules that can be passed as parameters or returned as results by a parameterized module are called higher-order modules.
A parameterized module is declared and used like a function. In its header a parameterized module declares formal module arguments. In a modular application, the arguments are applied to the parameterized module by binding actual module parameters to their corresponding formal module arguments. Parameterized modules are curried: partially applying them yields a new parameterized module depending on the still-unbound module arguments; a full application gives a concrete implementation module.
The module type expected by `MakeSet` is declared like this:
*ocaml
module Ordered = struct
module type Type =
sig
type t
val compare: t -> t -> int
end
end
*
This is essentially a total order relation that `MakeSet` uses to implement set operations like membership and intersection efficiently.
Since we intend to store game positions in the transposition table, it makes sense to modify the `Board` module type so it must subtype the total order `Ordered.Type`. We also add the equality `type t = game` to ensure we compare game positions:
*ocaml
module type Board =
sig
type board
type moves
type game = {board: board; played: moves}
type strategy = (game -> unit) -> game -> unit
type t = game
val compare: t -> t -> int
end
*
With that change, `Board` is compatible with `Ordered.Type`.
VII. Bidirectional search
Now we want to be able to solve any kind of solitaire game. Often these games have an initial position and you must find a sequence of moves to reach a final position. Since the transposition table has already helped limit breadth, this time we’ll attack depth.
Bidirectional search eats the banana from both ends. We explore the search space forwards from the initial position, and simultaneously backwards from the final position. When the two searches meet, we have a solution. Each direction has its own transposition table. The searches meet when the intersection of the two tables is non-empty. Because the two searches progress together, they typically meet around half-depth — which halves the search depth. A small picture helps visualize different exploration strategies.
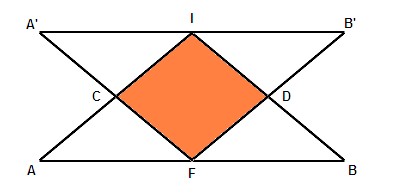
AI Course introduction Bidirectional search basic techniques
- Point I marks the initial position and point F the final position.
- Triangle IAB is the space to explore from I (forward search) before reaching F.
- Triangle FA’B’ is the space to explore from F (backward search) before reaching I.
- The orange diamond ICDF is the space to explore from I and F (bidirectional search) before they meet somewhere along segment CD.
This picture understates the efficiency of bidirectional search. A small numerical simulation shows the savings:
suppose each move offers only 2 choices;
suppose the solution depth is 20 moves;
with direct search you’d explore $2^{20} = 1,048,576$ positions;
with bidirectional search you meet at half-depth, exploring $2^{10}$ positions in each direction, so $2^{10}+2^{10} = 2048$ positions in total;
result: bidirectional search explores $2^{20} / 2^{11} = 2^{9} = 512$ times fewer positions — i.e., it’s about 512 times faster than an untargeted search.
Our solver module for solitaire games is a higher-order module like this:
*ocaml
module Solver (B: Board) (Set: Mutable.Set with type item = B.game) =
struct
let play p sa = …
let solve p zip ga gb = …
end
*
It expects:
a module that implements a board type;
a module implementing a transposition table (MakeSet will do) whose item type is a game position (`type item = B.game`).
It provides two functions we still need to implement:
`play`, which builds a transposition table `sb` that goes one move beyond table `sa`;
`solve`, which finds all paths from position `ga` to position `gb` using strategy `p`.
`play` is a bit twisted: for a given set `sa`, it iterates over it and adds (`Set.add`) all positions generated by strategy `p` to an initially empty set `sb` (`Set.empty`):
*ocaml
let play p sa =
let sb = Set.empty () in
Set.iter (fun g -> p (fun x -> Set.add x sb) g) sa; sb
*
At the end `play` returns `sb` as the new transposition table. `solve` alternates between `even` and `odd` to expand either the forward search (table `sa`) or the backward search (table `sb`). It stops when the intersection between `sa` and `sb` is non-empty.
*ocaml
let solve p zip ga gb =
let rec even sa sb =
match Set.zip_intersect zip sa sb with
| [] -> odd (play p sa) sb
| l -> l
and odd sa sb =
match Set.zip_intersect zip sa sb with
| [] -> even sa (play p sb)
| l -> l
in
even (Set.singleton ga) (Set.singleton gb)
*
Given the small amount of code we wrote, you might find it hard to believe we’ve solved solitaire games — but broadly speaking, we have.
Bidirectional Search Infographic Easy AI Course Introduction
VII-A. Example: the Rubik’s Cube
The classic Rubik’s Cube would be a bit tedious for this example. To simplify notation, we’ll use the Pocket Cube — the 2x2x2 version.

We’ll make a `PocketCube` module that implements our `Board` module type. It’s a 3D board!
*ocaml
module PocketCube =
struct
…
end
*
The PocketCube has eight small cubes. We’ll imagine one is fixed (the top-front-left), leaving seven mobile cubes labeled C1..C7.
*ocaml
type cubie =
| C1 | C2 | C3 | C4 | C5 | C6 | C7
*
Each cubie has three orientations:
*ocaml
type orientation =
| O1 | O2 | O3
*
The full state is a 7-tuple of cubies and a 7-tuple of orientations.
*ocaml
type ‘a septuple =
‘a ‘a ‘a ‘a ‘a ‘a ‘a
type board =
cubie septuple orientation septuple
*
Possible moves are quarter turns front/back/left/right/up/down clockwise. We also define `moves` (the list of moves) and `game` (positions).
*ocaml
type move =
| Front | Back | Left | Right | Up | Down
type moves =
move list
type game =
{board: board; played: moves}
*
Orientation is rotated forward or backward:
*ocaml
let ror = function
| O1 -> O2 | O2 -> O3 | O3 -> O1
let rol = function
| O1 -> O3 | O2 -> O1 | O3 -> O2
*
The initial PocketCube state (which will be the target final state for solving):
*ocaml
let initial = {
board = (C1,C2,C3,C4,C5,C6,C7),(O1,O1,O1,O1,O1,O1,O1);
played = [] }
*
The effect of the six rotations on a game `g`:
*ocaml
let right g =
let (c1,c2,c3,c4,c5,c6,c7),(o1,o2,o3,o4,o5,o6,o7) = g.board in {
board = (c2,c5,c3,c1,c4,c6,c7),(ror o2,rol o5,o3,rol o1,ror o4,o6,o7);
played = Right::g.played }
let back g =
let (c1,c2,c3,c4,c5,c6,c7),(o1,o2,o3,o4,o5,o6,o7) = g.board in {
board = (c1,c2,c3,c5,c6,c7,c4),(o1,o2,o3,ror o5,rol o6,ror o7,rol o4);
played = Back::g.played }
let down g =
let (c1,c2,c3,c4,c5,c6,c7),(o1,o2,o3,o4,o5,o6,o7) = g.board in {
board = (c1,c3,c6,c4,c2,c5,c7),(o1,o3,o6,o4,o2,o5,o7);
played = Down::g.played }
let left g =
let (c1,c2,c3,c4,c5,c6,c7),(o1,o2,o3,o4,o5,o6,o7) = g.board in {
board = (c4,c1,c3,c5,c2,c6,c7),(ror o4,rol o1,o3,rol o5,ror o2,o6,o7);
played = Left::g.played }
let front g =
let (c1,c2,c3,c4,c5,c6,c7),(o1,o2,o3,o4,o5,o6,o7) = g.board in {
board = (c1,c2,c3,c7,c4,c5,c6),(o1,o2,o3,ror o7,rol o4,ror o5,rol o6);
played = Front::g.played }
let up g =
let (c1,c2,c3,c4,c5,c6,c7),(o1,o2,o3,o4,o5,o6,o7) = g.board in {
board = (c1,c5,c2,c4,c6,c3,c7),(o1,o5,o2,o4,o6,o3,o7);
played = Up::g.played }
*
`scramble` mixes a game position `g` with `n` random rotations:
*ocaml
let rec scramble g n =
if n = 0 then g
else
scramble
( match Random.int 6 with
| 1 -> front g | 2 -> back g
| 3 -> left g | 4 -> right g
| 5 -> up g | n -> down g )
(n-1)
*
`inverse` undoes a rotation and `zip` rebuilds a sequence of rotations from one sequence starting at initial `ga` and another leading to `gb`:
*ocaml
let inverse = function
| Front -> Back | Back -> Front
| Left -> Right | Right -> Left
| Up -> Down | Down -> Up
let zip ga gb =
List.rev_append (List.map inverse gb.played) ga.played
*
`player` is a simplistic strategy: try the six rotations:
*ocaml
type strategy =
(game -> unit) -> (game -> unit)
let player : strategy = fun f g ->
f (front g); f (back g);
f (left g); f (right g);
f (up g); f (down g)
*
What remains is to satisfy the `Solver` constraint `type item = Board.game`:
*ocaml
type t = game
let compare : t -> t -> int =
fun ga gb -> Pervasives.compare ga.board gb.board
*
VIII. Implementing the Pocket Cube solver
What we have is a general solver from which we’ll derive a Pocket Cube solver. That’s the point of parameterized modules: a useful module is obtained by instantiating a parameterized module. A parameterized module makes it possible to produce useful modules like a class produces useful objects.
First, a small alias to simplify notation:
*ocaml
module Cube = PocketCube
*
Now we create `CubeSolver`, a solver for the Pocket Cube. To make a cube solver from the generic solver, pass `Cube` as the first parameter and a transposition table for `Cube` as the second:
*ocaml
module CubeSolver = Solver(Cube)(Mutable.MakeSet(Cube))
*
This way of creating a new module by providing argument modules to a parameterized module is called modular application.
Initialize the random number generator:
*ocaml
Random.self_init ()
*
Create a pocket-cube scrambled with 60 random rotations:
*ocaml
# let scrambled = Cube.scramble Cube.initial 60;;
*
This returns:
*
val scrambled : Cube.game =
{Cube.board =
((Cube.C3, Cube.C4, Cube.C2, Cube.C7, Cube.C1, Cube.C5, Cube.C6),
(Cube.O2, Cube.O1, Cube.O3, Cube.O1, Cube.O1, Cube.O3, Cube.O2));
Cube.played =
[Cube.Left; Cube.Left; Cube.Left; Cube.Up; Cube.Front; Cube.Front;
Cube.Up; Cube.Down; Cube.Right; Cube.Right; Cube.Left; Cube.Right;
Cube.Left; Cube.Right; Cube.Right; Cube.Up; Cube.Down; Cube.Up;
Cube.Front; Cube.Front; Cube.Left; Cube.Back; Cube.Left; Cube.Right;
Cube.Up; Cube.Up; Cube.Up; Cube.Back; Cube.Front; Cube.Up; Cube.Back;
Cube.Front; Cube.Up; Cube.Down; Cube.Up; Cube.Front; Cube.Left;
Cube.Left; Cube.Down; Cube.Front; Cube.Front; Cube.Left; Cube.Left;
Cube.Front; Cube.Up; Cube.Left; Cube.Down; Cube.Right; Cube.Back;
Cube.Front; Cube.Left; Cube.Up; Cube.Front; Cube.Right; Cube.Front;
Cube.Down; Cube.Back; Cube.Left; Cube.Right; Cube.Right]}
*
Note: the `Cube.played` field contains the list of moves needed to reconstruct the initial cube.
We force forgetting the path back to the initial position:
*ocaml
# let scrambled_blanked = {scrambled with Cube.played = []};;
*
Result:
*
val scrambled_blanked : Cube.game =
{Cube.board =
((Cube.C3, Cube.C4, Cube.C2, Cube.C7, Cube.C1, Cube.C5, Cube.C6),
(Cube.O2, Cube.O1, Cube.O3, Cube.O1, Cube.O1, Cube.O3, Cube.O2));
Cube.played = []}
*
Running the bidirectional search solver shows there were four ways to reach this configuration in 10 moves rather than the 60 random moves generated:
*ocaml
# CubeSolver.solve Cube.player Cube.zip scrambled_blanked Cube.initial;;
*
Result:
*
– : Cube.move list list =
[[Cube.Front; Cube.Up; Cube.Back; Cube.Left; Cube.Left; Cube.Down; Cube.Down;
Cube.Right; Cube.Up; Cube.Up];
[Cube.Up; Cube.Right; Cube.Down; Cube.Down; Cube.Back; Cube.Right;
Cube.Front; Cube.Right; Cube.Up; Cube.Back];
[Cube.Down; Cube.Down; Cube.Right; Cube.Back; Cube.Down; Cube.Down;
Cube.Left; Cube.Left; Cube.Up; Cube.Back];
[Cube.Front; Cube.Down; Cube.Right; Right; Cube.Down; Cube.Down;
Cube.Front; Cube.Left; Cube.Up; Cube.Up]]
*
Thanks to the transposition table, the search is very fast; regardless of the configuration, it takes little more than a second on the bytecode interpreter. Even though the number of possible configurations is 3,674,160, bidirectional search only explores a small fraction of that space.
IX. Conclusion
With this introduction I’ve surveyed techniques for solving solitaire games.
These techniques remain relevant for multiplayer strategy games. However, two-player games are more complex and require additional techniques — for those you’ll need to read and understand a good tutorial like Chess Programming.
Go is a popular game, especially in Asia, and its breadth makes it a challenge for many AI researchers. You can find a state-of-the-art review in the article MoGo, master of Go?.
Easy AI Course Modular Software Architecture simple compose AI prompt Design
X. Discussion on higher-order modules
I also hope I convinced you that modeling with higher-order modules is an effective way to factor solutions so you don’t have to repeatedly solve problems you solved before. Of course that generality isn’t free: it has an intellectual cost — it’s harder to design a higher-order module than to write code that does the same job for a single, fixed situation.
You usually must choose between two pitfalls:
- Over-engineering: anticipating complexity that never appears because in practice you only encounter simple cases;
- Patchwork: realizing too late that quick-and-dirty solutions won’t scale when the specification complexity grows.
With AI for two or more players you can be sure specifications will grow considerably. The risk is patchwork that prevents reuse of a toolbox (move generation, transposition table) — which you’d really want when adding sophisticated features like alpha-beta, heuristics and iterative deepening. What you want instead is to assemble elements from a set of parameterizable components. Higher-order modules allow that with a level of precision, safety and generality that’s hard to reach with similar approaches. Other approaches tend to either increase confidence without improving technical quality, or make compromises that sacrifice some technical qualities to gain margin for others.
Advantages of higher-order modules over classical modeling (Design Patterns or UML):
You capture the design inside the programming language itself (Objective Caml), so:
- You benefit from an extremely strict type system that can invalidate inconsistencies at design time;
- The transition to implementation is immediate and unsurprising since the design language is the implementation language;
- You avoid confusion between specification and communication — with higher-order modules, the disillusion comes sooner and stronger (Objective Caml doesn’t allow unsafe casting). You can’t just draw pretty boxes or bubbles and pretend that’s software genius; with higher-order modules that bluff is exposed quickly.
- Unlike Design Patterns, you don’t fight the natural paradigm of the implementation language or try to perform contortions. In the end you don’t lose safety (quite the opposite). The loss in readability is only due to the higher level of specification — there’s no “ravioli coding” where you’must follow endless execution meanders hidden by supposed flexibility.
XI. Further reading
Parameterized modules exist in other languages beyond Objective Caml. The module language is largely independent of the type system, and any modular language could be given parameterized modules. For now, though, this remains a privilege of ML-family languages. Still, sophisticated languages on platforms like the JVM are starting to emerge that could simulate parameterized modules.
Below is an overview of web resources on parameterized modules in the two languages where they are best established.
Standard ML (SML) :
Objective-Caml :
- OCaml: The module system
- The OCaml module system
- Implementation as ML Functors
- Tilings as a programming exercise
XII.Afterword — From Concepts to Mastery
You’ve just read a clear, compact tour of the elementary techniques used to build AIs for abstract strategy and puzzle games: move generation, transposition tables, bidirectional search, higher-order modules and a worked PocketCube example. Now I’ll extend that material as a teacher, not just repeating facts but turning them into a learning path, practical lab exercises, debugging heuristics, design recipes, and a set of disruptive thought experiments that will stretch how you think about game AI and modular design.
How to feel the search space
Before coding, develop an internal picture of what your program will explore.
-
Imagine each legal position as a node in an invisible graph; legal moves are edges. The search problem is a graph traversal from one node (the current position) to target nodes (winning, solved, or improved positions).
-
Two dimensions govern complexity: width (branching factor: how many moves per position?) and depth (how many moves to reach interesting outcomes?). These determine the volume of nodes reachable within a budget.
-
Your algorithms are ways to carve this graph into a tractable subgraph that keeps relevant nodes and eliminates redundancy and dead ends.
Why this matters: when you can visualize where waste lives (symmetries, reversals, repeated states), the right fixes become obvious: canonicalization, hashing, transposition tables, pruning, bidirectional search
Essence in plain language — what really matters
Think of an AI for a board or puzzle game as a detective exploring possibilities. The detective’s two problems are:
-
Too many places to look at once (width). If every move opens dozens or hundreds of alternatives, the detective is overwhelmed.
-
Too many steps to the solution (depth). If the solution requires hundreds of steps, checking every route becomes impossible.
Good AI is not raw force. It’s smart pruning — the detective uses memory (transposition table), clever search patterns (bidirectional search), and modular tools so you can reuse the same detective for many puzzles. Higher-order modules are like building a detective kit that can be assembled for each new case without re-inventing binoculars and fingerprint kits.
Key takeaways:
-
Always measure whether your game is wide, deep, or both. That determines the best weapon: breadth reduction (symmetry removal, transposition tables) or depth reduction (bidirectional search, heuristics, iterative deepening).
-
Favor modularity early. Design reusable interfaces (game state, move generator, strategy, transposition set). This saves time when you add alpha-beta, heuristics, or parallelism later.
-
Start simple (solitaire puzzles), not with chess or Go. The basic tools generalize — but complexity multiplies quickly.
Debugging checklist (practical fallbacks when search misbehaves)
When your solver is slow or incorrect, run this checklist in order:
-
Correctness first: Are move generation and inverse moves correct? Often bugs appear in edge cases (wrapping indices, orientation flips). Add property tests that scramble and then inverse-apply moves to restore the original board.
-
Canonicalization: Are equivalent states hashed identically? Implement a canonical form (e.g., sorted representation or normalized orientation).
-
Transposition hash collisions: If you use small hashes, collisions create silent errors; increase hash size or use exact equality checks upon hash matches.
-
Memory vs time tradeoff: Is memory exhausted? Consider memory-light alternatives (iterative deepening, IDA*).
-
Strategy explosion: Are you generating trivial repeated sequences (A then A-rev)? Add move ordering or disallow immediate inverse moves.
-
Profiling: Use a profiler to find hotspots — generator, comparator, hash function. Optimize accordingly.
-
Decomposition test: Can you factor the board into independent subproblems? If yes, solve them separately or apply search partitioning.
From solitaire to two-player games — main conceptual shifts
Two-player games add adversarial reasoning: every move by your AI must anticipate the opponent. That surface change implies structural changes:
-
Replace single-agent search with minimax trees; use alpha-beta pruning to reduce branches.
-
Add evaluation functions (heuristics that score nonterminal positions) because exhaustive search is infeasible.
-
Introduce iterative deepening (IDA) and move ordering (order by heuristic, killer moves, history heuristics) to maximize alpha-beta efficiency.
-
Add time management: for interactive play, you must return a move before a time budget expires — iterative deepening lets you always have a best-so-far move.
The modular, higher-order approach helps here: keep the same move generation and transposition primitives but swap in a new search driver (minimax+alpha-beta) and evaluation module.
Design patterns that actually help (practical, not theoretical)
-
Canonicalizer pattern: central place to normalize a board to reduce symmetric states.
-
Move Generator Facade: single interface that hides move internals (keeps search code game-agnostic).
-
Pluggable Transposition: allow swap of set implementations (hashset, tree, disk-backed) without changing solver.
-
Strategy as first-class function: strategies as functions
(add_fn -> game -> unit)keep the solver generic and let you inject different expansion policies. -
Iterative Driver: a driver that wraps any search algorithm into an iterative deepening loop, adding time control.
Research & project directions (where to invest learning time next)
-
Large branching games (Go-like): study Monte Carlo Tree Search (MCTS) and UCT; combine with learned priors (policy/value nets).
-
Learning heuristics: use offline self-play to learn evaluation functions (neural networks) that replace hand-crafted heuristics.
-
Hybrid symbolic+learned agents: use a symbolic search core augmented with small learned modules for move ordering and pruning decisions.
-
Module composability: formalize a small DSL to describe board types and auto-generate module stubs.
Disruptive thinking
These are deliberately provocative to push new designs.
-
What if the search itself were a learned policy that decides dynamically which subgraph to explore, rather than following fixed heuristics? (A learned meta-controller that shapes classical search.)
-
What if games were compressed into a latent representation where search is done in the latent space and then decoded into human-readable moves? (Search in compressed manifolds.)
-
What if a game engine published an API of invariants (symmetries, reversibility, conserved quantities) and solvers could auto-compose these invariants to prune their search? (Game-descriptive metadata driving automatic optimizations.)
Hypothesis 1 → Opportunity: Meta-search as learned controller
Consumers: developers building general puzzle solvers; researchers optimizing search budgets.
Radical ideas:
-
Search-RL: train an RL agent that, given a position and search budget, chooses which branches to expand next. Combine with imitation learning from near-optimal searches.
-
Budgeted Expert Mixture: ensemble where shallow exhaustive search is used on some subproblems and deep heuristic search on others, with a learned selector deciding which.
-
Adaptive Transposition Policies: a controller that dynamically decides which states to keep in the transposition table vs evict based on downstream expected utility.
Hypothesis 2 → Opportunity: Latent-space planning
Consumers: AI researchers, generative modelers, compact solvers.
Radical ideas:
-
Autoencoder Solvers: train an encoder that projects board states into a dense latent; run MCTS or heuristic search there, then decode a latent path into moves. This reduces branching by collapsing equivalent states.
-
Latent Heuristic Synthesis: use latent distances as heuristics; distances in the latent space approximate true solution distances.
-
Progressive Refinement: search coarse-to-fine in latent layers — coarse plan in high abstraction, refine into concrete moves (similar to hierarchical planning).
Hypothesis 3 → Opportunity: Machine-readable game metadata
Consumers: game engine designers and platform vendors.
Radical ideas:
Invariant Registry: a standard schema where a game declares symmetries, conserved invariants, and move commutativity; solvers plug this registry to auto-apply reductions.
Solver Marketplace: game authors provide metadata and a small solver template; third-party solvers automatically compose with metadata to yield optimized AI plug-ins.
Compiler-assisted pruning: a tooling pipeline that ingests game rules and emits optimized canonicalizers and partial evaluators.
The earlier article gave you the essential toolset — here you have the extended laboratory and the conceptual scaffolding to convert that toolkit into mastery.

Easy AI Course PocketCube Algorithm Artistry





