AI Course

Fuzzy logic introduction

Posted by aistore

20 September 2025

On 20 September 2025

0

Fuzzy logic is an extension of classical logic that allows for the modeling of imperfections in data, and in some ways, it more closely resembles the flexibility of human reasoning.

In this introductory course, we’ll begin by defining the basic concepts of fuzzy logic and then explain them with an example that we’ll use throughout the course. The example is: deciding on the tip amount after a restaurant meal based on the perceived quality of the service and food. This is a classic case often used to introduce fuzzy logic.

Prerequisites: You’ll need a foundational knowledge of set theory and classical (Boolean) logic.

Table of Contents

Toggle

Introduction

Fuzzy logic is an extension of Boolean logic proposed by Lotfi Zadeh in 1965. It’s based on his fuzzy set theory, which generalizes classical set theory. By introducing the concept of degree into condition evaluation, a condition is no longer simply “true” or “false,” but can exist in an intermediate state. This makes reasoning more flexible and capable of handling vague and uncertain information.

One advantage of fuzzy logic is that its rules are often expressed in natural language. For example, a driver (who is very careful about their license) might follow rules like these:

• If the red light is on… the car is going fast… and it’s close… → I’ll brake hard.
• If the red light is on… the car is going slow… and it’s far away… → I’ll maintain my speed.
• If the orange light is on… the car is going at a medium speed… and it’s far away… → I’ll brake gently.
• If the green light is on… the car is going slow… and it’s close… → I’ll accelerate.

Intuitively, our brains don’t process these input variables with precise values, but rather with approximate assessments. This corresponds perfectly to the fuzzy logic concept of “degree of satisfaction” for a condition.

In this course, we’ll progressively design a fuzzy inference system with the goal of determining the tip amount based on the quality of service and food.

 

Fuzzy Subsets

Fuzzy logic is built upon fuzzy set theory, which is a generalization of classical set theory. In academic literature, the terms “fuzzy subset” and “fuzzy set” are often used interchangeably. Classical sets are also referred to as “crisp sets,” in contrast to “fuzzy” ones. Similarly, classical logic is also known as Boolean or two-valued logic.

For example, here’s a function that describes the membership function for the fuzzy subset “good service quality”:

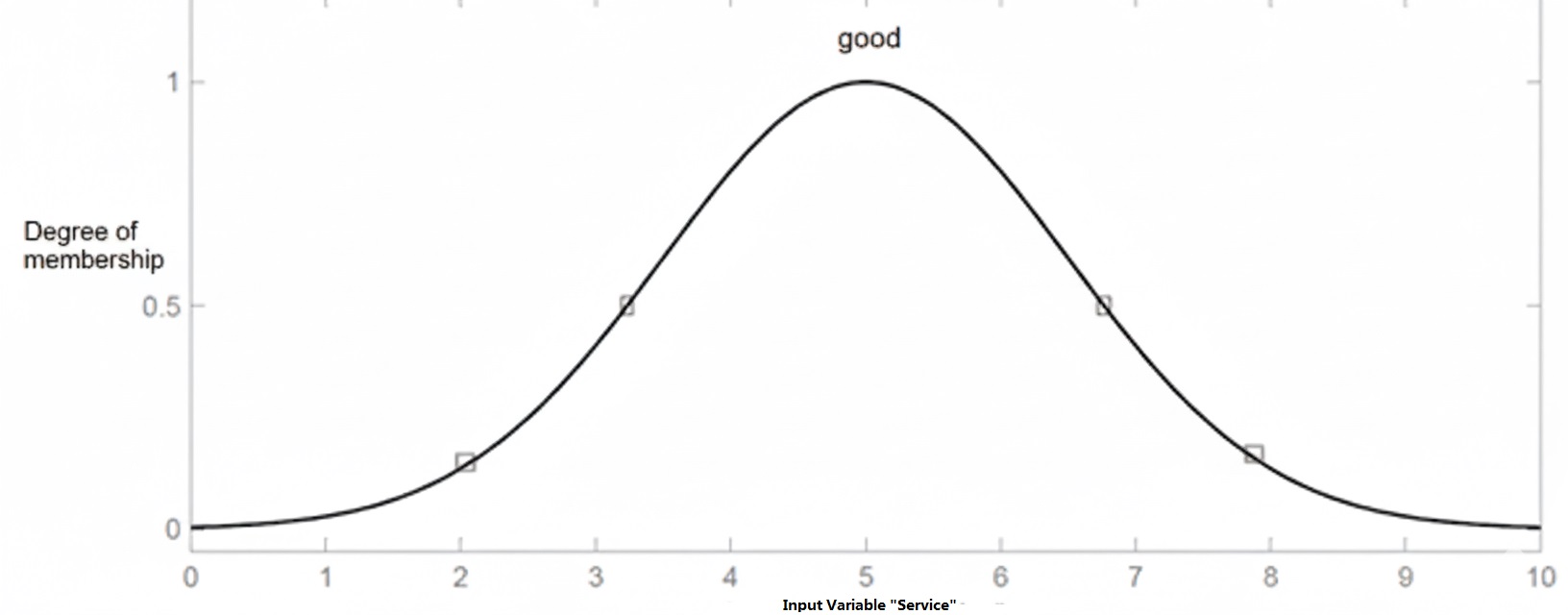
Membership function characterizing the subset ‘good’ of service quality

Definition: A fuzzy subset A of a set X is defined by a membership function fA​:X→[0,1]. This function is the fuzzy equivalent of a classical set’s characteristic function.

For our tipping example, we need to define membership functions for fuzzy subsets across three types of variables:

• Input 1: Service Quality → Fuzzy subsets: Poor, Good, Excellent
• Input 2: Food Quality → Fuzzy subsets: Bad, Delicious
• Output: Tip Amount → Fuzzy subsets: Low, Medium, High

The shape of these membership functions is a design choice. They can be determined based on expert knowledge or statistical analysis and may take the form of S-functions, hyperbolic tangent functions, exponential functions, or Gaussian functions, among others.

This graph visually demonstrates the difference between a classical set and its corresponding fuzzy set for “delicious food”:

Graphical representation of a classic set and a fuzzy set

 

This diagram compares the two membership functions corresponding to the previous sets:

 

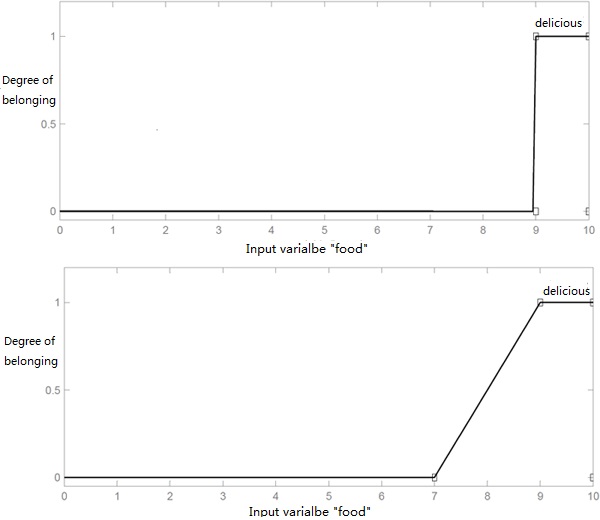
Comparison between the characteristic function of a classical set and the membership function of a fuzzy set 

To define the characteristics of fuzzy sets, we first redefine and extend the usual properties of classical sets.

Let $X$ be a set, $A$ a fuzzy subset of $X$, and μA​ its characteristic membership function.

DEFINITION: The height of $A$, denoted $h(A)$, corresponds to the supremum of the range of its membership function: h(A)=sup{μA​(x)∣x∈X}.

DEFINITION: $A$ is said to be normalized if and only if $h(A)=1$. In practice, it is extremely rare to work with non-normalized fuzzy sets.

DEFINITION: The support of $A$ is the set of elements in $X$ that belong to $A$ even in the slightest degree. In other words, it is the set supp(A)={x∈X∣μA​(x)>0}.

DEFINITION: The core of $A$ is the set of elements in $X$ that belong to $A$ completely. In other words, it is the set core(A)={x∈X∣μA​(x)=1}. By construction, $\text{core}(A)\subseteq \text{supp}(A)$.

DEFINITION: An $\alpha$-cut of $A$ is the classical subset of elements with a degree of membership greater than or equal to $\alpha$: α-cut(A)={x∈X∣μA​(x)≥α}.

Here is another membership function for a medium tip, with the properties above illustrated:

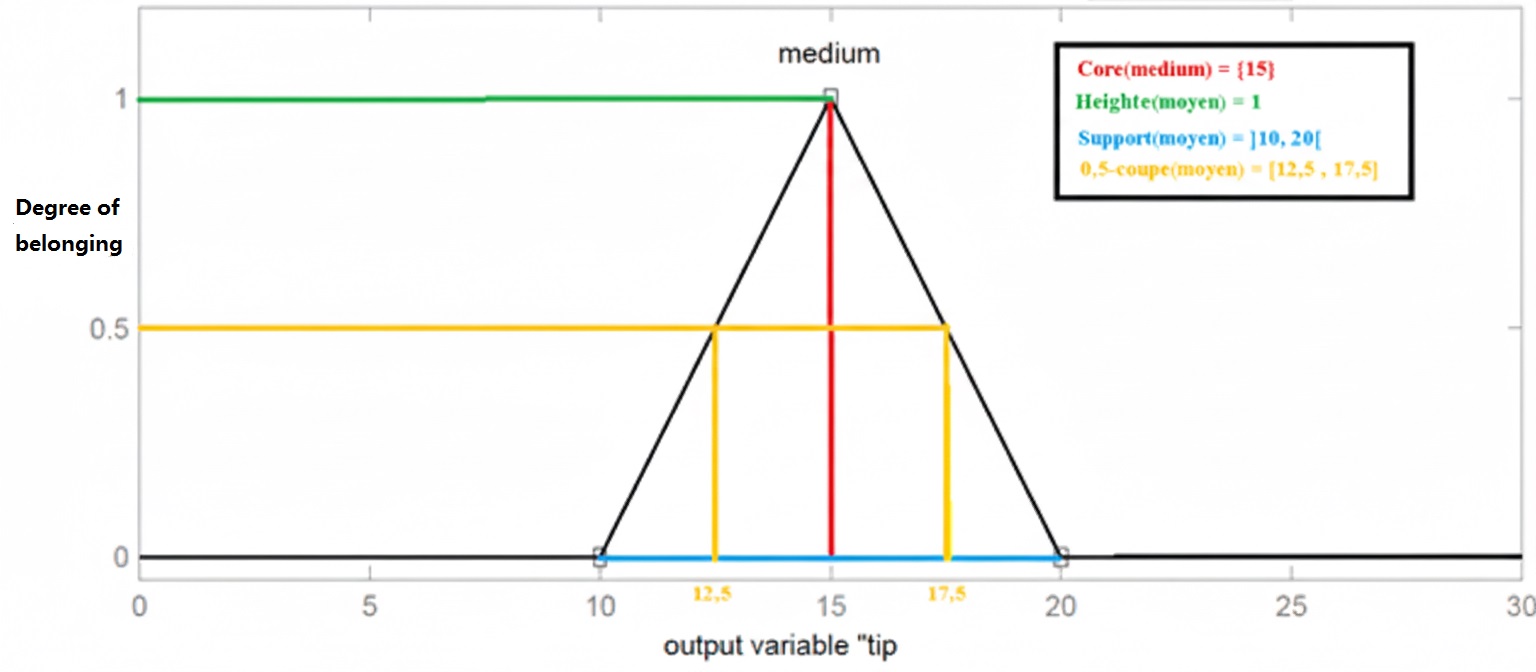
AI Course Properties of a fuzzy set

 

Linguistic Variables

With membership functions, we can define fuzzy systems using natural language. A linguistic variable provides a way to link numerical variables with fuzzy subsets.

Definition: A linguistic variable is a triplet (V,X,Tv​), where $V$ is a variable (e.g., service quality or tip amount), $X$ is its range of values, and Tv​ is a set of its corresponding fuzzy subsets.

Examples:

• Service Quality → {Poor, Good, Excellent}
• Food Quality → {Bad, Delicious}
• Tip Amount → {Low, Medium, High}

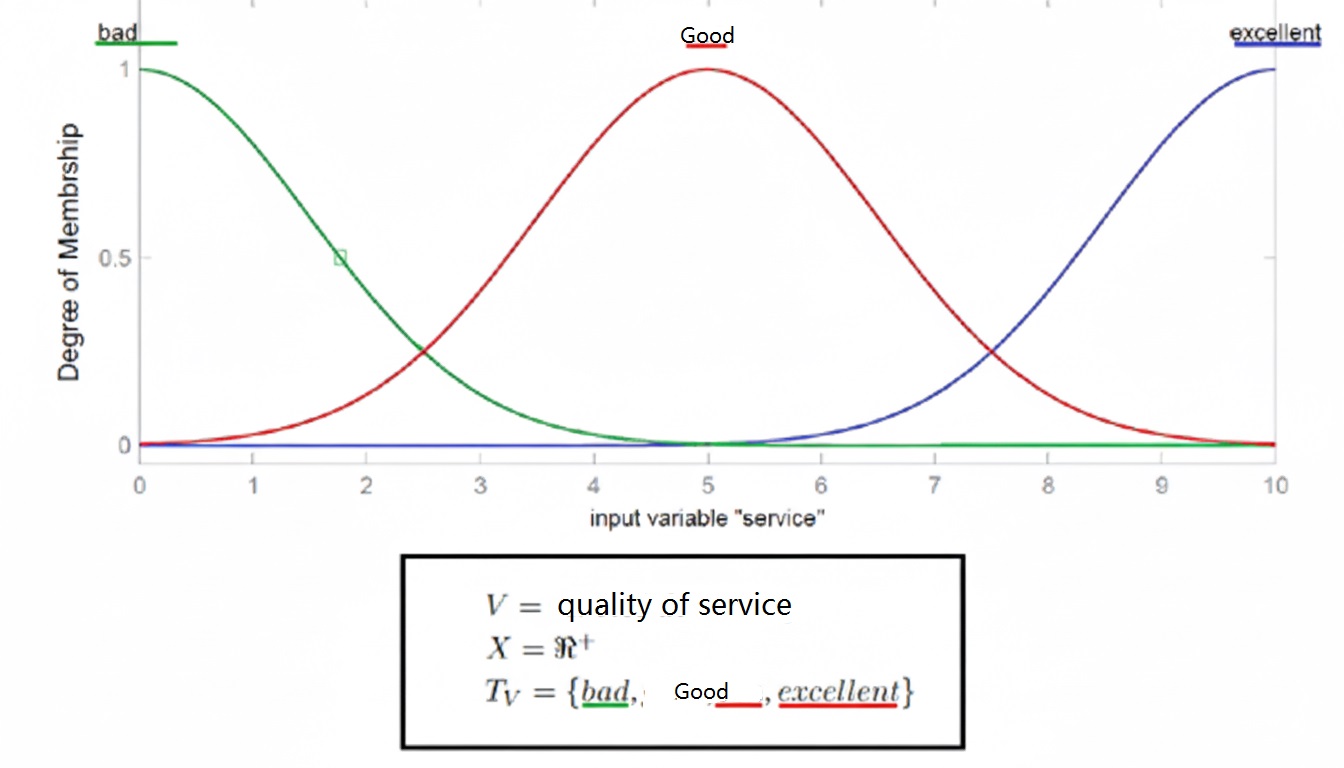
Linguistic variable service quality

 

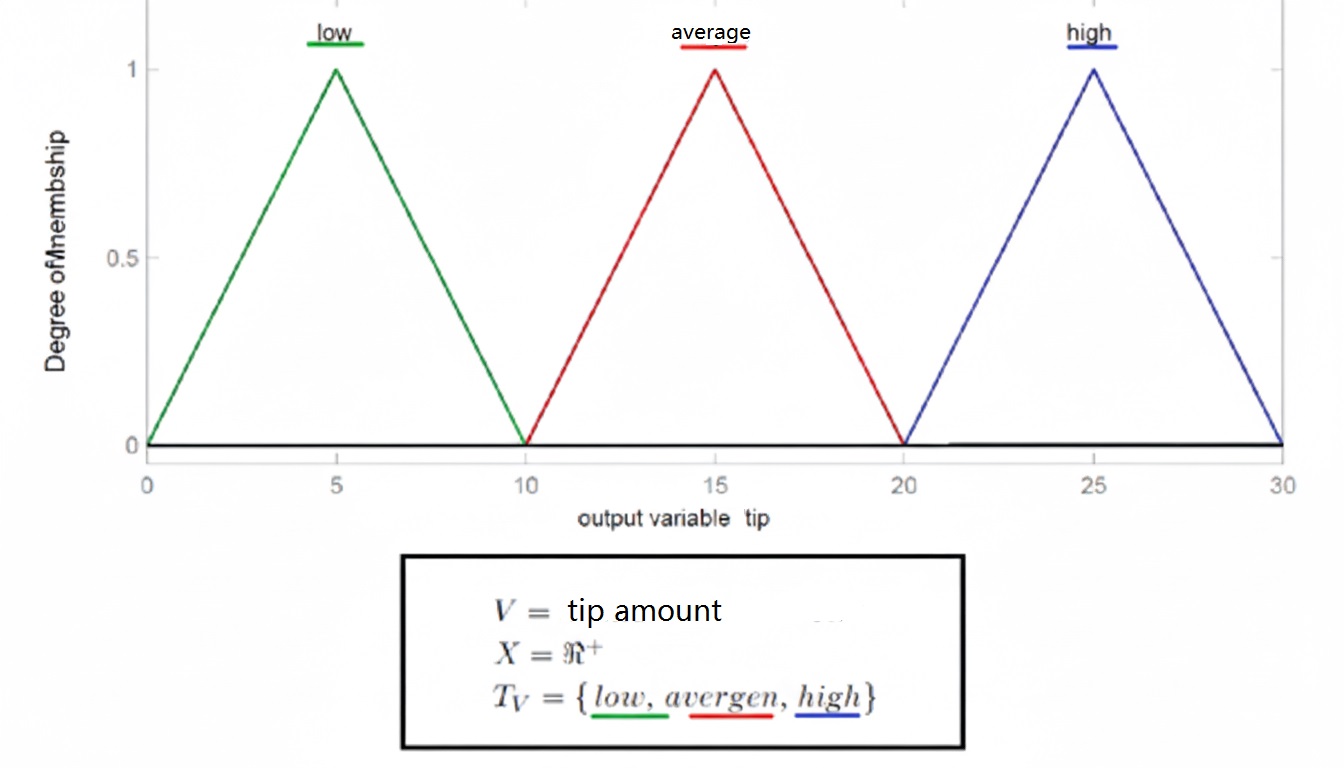
Linguistic variable tip amount

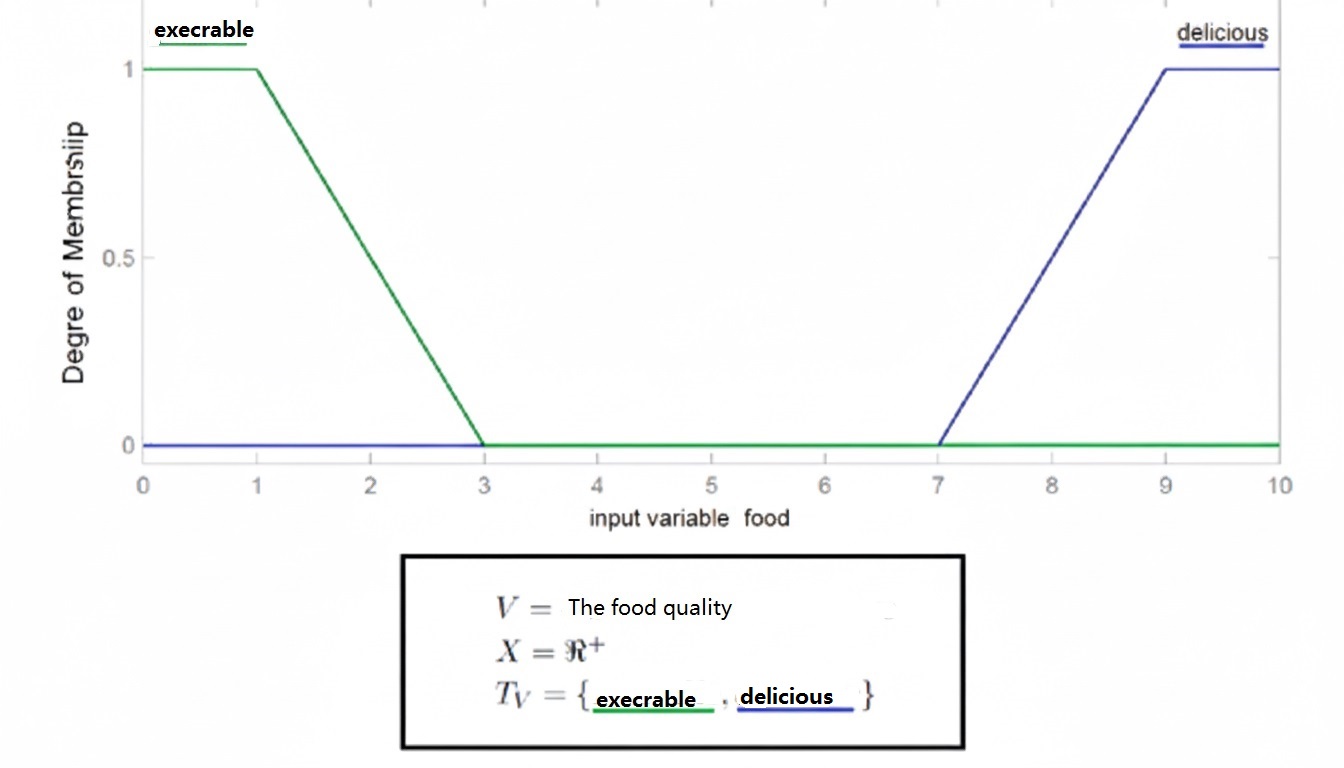
Linguistic variable the quality of the food

Fuzzy Operators

To work with fuzzy sets, we need to redefine the classical set operators (AND, OR, NOT) so they can handle membership values between 0 and 1.

There are two common types of operators:

Zadeh Operations (Most Common)

• Intersection (A ∩ B): min(μA​(x),μB​(x))
• Union (A ∪ B): max(μA​(x),μB​(x))
• Complement (Aˉ): 1−μA​(x)

Probabilistic Operations

• Intersection (A ∩ B): μA​(x)×μB​(x)
• Union (A ∪ B): μA​(x)+μB​(x)−μA​(x)×μB​(x)
• Complement (Aˉ): 1−μA​(x)

These operations maintain commutativity, associativity, and distributivity. However, they differ from classical logic in two key ways:

• The law of the excluded middle does not hold: A∪Aˉ=X
• An element can partially belong to both A and not A at the same time: A∩Aˉ=∅

Fuzzy Inference

In classical logic, inference follows this pattern:

If $p\to q$ $p$ is true $\to$ $q$ is also true

In fuzzy logic, fuzzy inference (also known as approximate reasoning) is based on fuzzy rules expressed in natural language, using the linguistic variables we defined earlier. A fuzzy rule typically has the following form:

“If $x\in A$ and $y\in B$, then $z\in C$”

where $A$, $B$, and $C$ are fuzzy sets.

For example, a rule might be: “If (food quality is delicious), then (the tip will be high).”

The degree to which the variable “tip” belongs to the fuzzy set “high” depends on the degree to which the premise holds—that is, the membership value of the variable “food quality” in the fuzzy set “delicious.” The core idea is: the more a proposition in the premise is validated, the more the suggested output action in the conclusion should be respected. To determine the truth value of the fuzzy proposition “the tip will be high,” we must define fuzzy implication (the fuzzy implication relation).

Like other fuzzy operators, fuzzy implication doesn’t have a single, universal definition. The designer of a fuzzy system must choose from a variety of existing fuzzy implications or define one manually. The two most common definitions used in practice are:

It’s worth noting that these two implications do not generalize classical implication (i.e., they don’t include it as a special case). While other fuzzy implications that do generalize classical implication exist, they are less commonly used.

If we choose the Mamdani implication for the rule “If (food quality is delicious), then (the tip will be high),” and the food quality is rated as 8.31 on a 10-point scale, we get the following result:

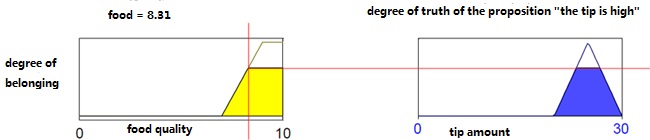
AI Course Example of fuzzy implication

The outcome of applying a single fuzzy rule depends on three factors:

• The chosen fuzzy implication definition.
• The membership function of the fuzzy set in the rule’s conclusion.
• The degree of truth (membership) of the proposition in the rule’s premise.

Since we’ve defined fuzzy AND, OR, and NOT operators, the premise of a fuzzy rule can be composed of several fuzzy propositions combined with a conjunction (AND). The entire set of rules for a fuzzy system is called the decision matrix. Here is our decision matrix for the tipping example:

• If service is poor or food is bad, then the tip is low.
• If service is good, then the tip is medium.
•  If service is great or food is delicious, then the tip is high.

Now, we’ll use these three rules from our decision matrix to perform inference. This will result in three fuzzy sets for the tip amount. We then aggregate them into a single fuzzy set, typically using the MAX operator. The following diagram illustrates this aggregation:

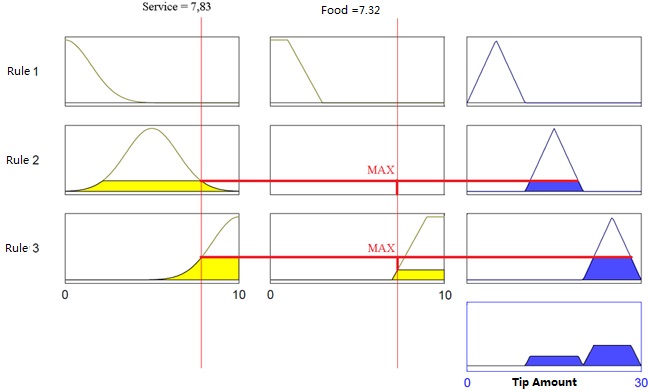
AI Course Example of fuzzy involvement using the decision matrix

Defuzzification using the maximum average method 

Defuzzification using the centroid method (COG)

COG defuzzification, while more computationally intensive, avoids the discontinuities that can occur with the MM method. Some research focuses on finding less complex alternatives that still maintain performance. As we saw when applying MM versus COG to our example, the choice of defuzzification method can have a significant impact on the final decision.

Conclusion + Keywords

Throughout the definition process, we’ve seen that fuzzy system designers must make many choices. These choices are typically based on expert advice or statistical analysis of historical data, especially when defining membership functions and the decision matrix.

Here is a synoptic overview of a fuzzy system:

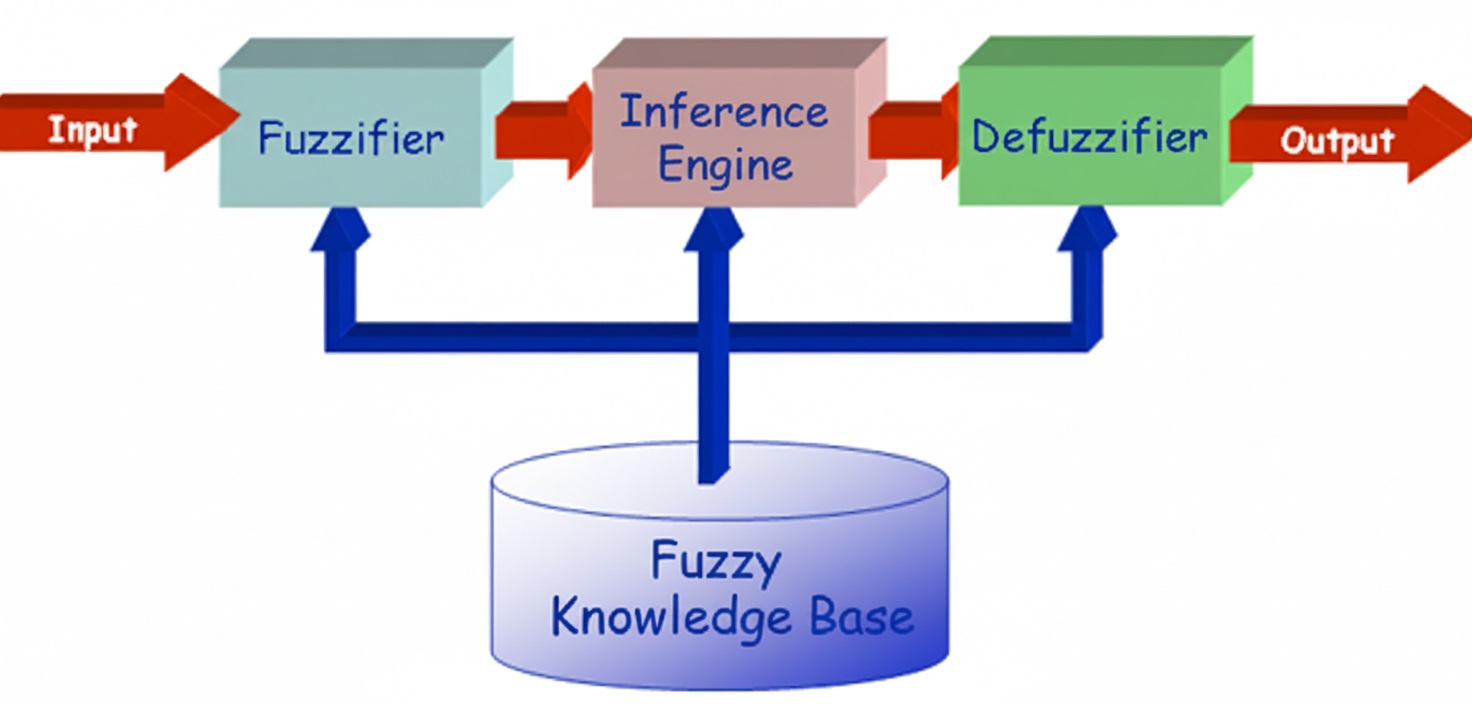
AI course introduction synoptic overview of a fuzzy system

In our example:

• Input is “service quality rated 7.83/10, food quality rated 7.32/10.”
• Fuzzifier corresponds to the three linguistic variables: “service quality,” “food quality,” and “tip amount.”
• Inference engine is made up of the chosen fuzzy operators.
• Fuzzy knowledge base is the set of fuzzy rules.
• Defuzzifier is where the defuzzification method is applied.
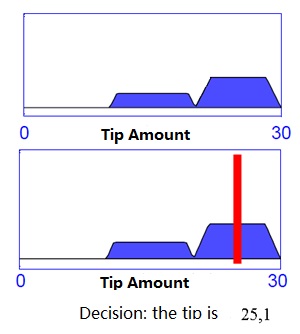
• Output is the final decision: “tip amount of 25.1.”

It’s interesting to compare the set of decisions from our fuzzy inference system with those from a classical logic system:

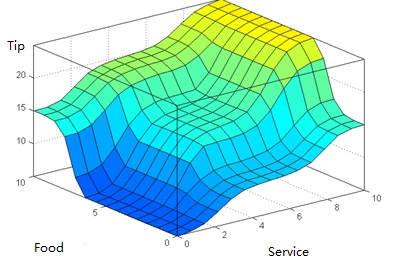
AI Course Set of decisions of a fuzzy system

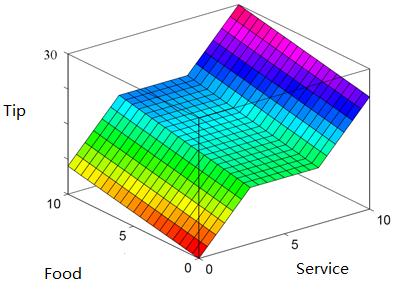
Easy Set of decisions of a system based on classical logic

The full power of fuzzy logic lies in its ability to create flexible, non-linear reasoning systems that produce decisions without sharp discontinuities. These decisions are closer to human behavior than the rigid, binary decisions of classical logic. Furthermore, expressing rules in a natural language offers many advantages, such as directly incorporating the expertise of non-computer specialists into the decision system or more subtly modeling certain aspects of natural language.

Keypoints

Fuzzy Logic Introduction

• Definition: An extension of Boolean logic that allows for “degrees” of truth between true/false.
• Prerequisites: Set theory + Boolean logic.

Core Concepts

• Fuzzy Set: Defined by a membership function $\mu (x)\in [0,1]$.
• Key Properties: Height, support, core, alpha-cut.
• Linguistic Variable: Described using natural language (e.g., Service Quality = Poor/Good/Excellent).

Operators

• Zadeh-type: min, max, $1-\mu (x)$.
• Probabilistic-type: product, algebraic sum.
• Does not satisfy the law of the excluded middle: A∪Aˉ=Universe.

Fuzzy Inference

• Rules: If…then… (natural language).
• Implication: Mamdani (min), Larsen (product).
• Aggregation: MAX method.

Defuzzification

• Mean of Maxima (MM): Simple but can be discontinuous.
• Center of Gravity (COG): More precise but computationally intensive.

Example: Tipping System

Inputs: Service Quality, Food Quality.

Output: Tip Amount (Low/Medium/High).

Rules:

• Poor or Bad $\to$ Low
• Good $\to$ Medium
• Excellent or Delicious $\to$ High

Conclusion

• Fuzzy logic = a mathematical approach to human-like reasoning.
• System design requires choosing: membership functions, operators, implication, aggregation, and defuzzification methods.

Easy AI Course Introduction fuzzy logic mindmap